전산유체역학을 이용한 소아 청소년 환자에서 상악 확장에 따른 상기도 내 공기 유동 변화 분석

Airflow analysis of pediatric upper airway following maxillary expansion using computational fluid dynamics

Article information

J Korean Dent Assoc. 2024;62(12):724-738

Publication date (electronic) : 2024 December 31

doi : https://doi.org/10.22974/jkda.2024.62.12.001

Tae-Hyun Kim ¹^,²^,³

, Kyung-Ho Lee ⁴^,⁵

, Dae-Woo Lee ¹^,²^,³

, Jae-Gon Kim ¹^,²^,³

, Jin-Mu Jung ⁴^,⁵

, Yeon-Mi Yang^,¹^,²^,³

¹Department of Pediatric Dentistry and Institute of Oral Bioscience, School of Dentistry, Jeonbuk National University

²Research Institute of Clinical Medicine, Jeonbuk National University

³Biomedical Research Institute, Jeonbuk National University Hospital

⁴Division of Mechanical Design Engineering Jeonbuk National University

⁵Hemorheology Research Institute, Jeonbuk National University

김태현¹^,²^,³

, 이경호⁴^,⁵

, 이대우¹^,²^,³

, 김재곤¹^,²^,³

, 정진무⁴^,⁵

, 양연미^,¹^,²^,³

¹전북대학교 치과대학 소아치과학교실 및 구강생체과학연구소

²전북대학교 임상의학연구소

³전북대학교병원 의생명연구원

⁴전북대학교 기계설계공학부

⁵전북대학교 혈유변학연구소

Corresponding Author Yeonmi Yang, DDS, PhD, Prof. Department of Pediatric Dentistry, School of Dentistry, Jeonbuk National University, 20, Geonji-ro, Deokjin-gu, Jeonju 54907, Republic of Korea Tel : +82-63-250-2212 / Fax : +82-63-250-2131 / E-mail : pedo1997@jbnu.ac.kr

Received 2024 September 2; Revised 2024 September 6; Accepted 2024 October 16.

Trans Abstract

Purpose

The objective of this study is to numerically analyze and visualize changes in airflow characteristics due to maxillary expansion in pediatric patients using computational fluid dynamics (CFD).

Materials and Methods

CBCT data from pediatric patients with an apnea-hypopnea index of over 1, habitual mouth breathing, and a constricted maxilla were used. For orthodontic treatment, maxillary expansion was conducted, and CBCT scans were taken before and after expansion. 3D models of the nasal airway, created from CBCT data, were converted into smoothed, mesh-divided models. CFD analysis was conducted and various parameters which can be used to evaluate flow obstruction, including pressure, velocity, and wall shear stress, were analyzed.

Results

In the patient with rapid expansion, constriction sites with high pressure, velocity, and wall shear stress distribution were identified in the anterior and posterior regions of the nasal cavity, while in the slow expansion patient, these high pressure, velocity, and wall shear stress distributed constriction sites were found in the anterior and mid-inferior regions of the nasal cavity. In both patients, after expansion, the flow-related variables that were highly distributed prior to expansion decreased, and their maximum values were also reduced.

Conclusion

CFD analysis enabled the identification of constriction sites within upper airway before undergoing expansion, and improvement in airflow was confirmed after both rapid and slow maxillary expansion in pediatric patients. CFD analysis on patient-specific upper airway models is expected to aid in precisely identifying the problematic areas of respiratory obstruction, thereby assisting in the selection of personalized treatment methods.

Keywords: Maxillary expansion; Upper airway; Computational fluid dynamics

I. 서론

비호흡 기능과 두개 안면 성장과의 관계는 골격적 성장에 있어 형태와 기능이 밀접한 연관 관계가 있음을 보여주는 대표적인 경우로써 Moss의 기능기질설에 의하면 비호흡은 저작 및 연하와 같은 다른 기능들과 상호작용하여 두개 안면 복합체의 적절한 성장과 발육을 가능하게 한다[1,2]. 호흡 중 비강을 통한 지속적인 공기의 흐름은 상악의 측방성장과 함께 구개골의 하방 이동을 위한 지속적인 자극을 유도한다[3]. 반면에 비강을 통한 호흡이 어려운 경우에는 줄어든 호흡을 보상하기 위해 구호흡이 발생하며 목과 연관된 두부 자세가 변화하게 된다. 혀는 낮게 위치하거나 전방으로 편위되며 구순의 기능은 약해지고 설골은 하방으로 위치하게 되면서 근육 활동의 불균형이 초래되고 치열을 포함한 치조골의 변화를 발생시킨다[4]. 이에 더해 비강 폐쇄로 인한 구호흡은 하악골의 후하방 회전, V자형 상악궁의 형성 및 구치부 반대교합의 주된 원인이 된다[3].

상악의 협착은 가장 흔히 발생하는 두개 안면 영역의 골격성 기형 중 하나로써 병인으로는 구순 구개열과 같은 유전적인 요인 외에도 비호흡 장애로 인한 구호흡, 저위설을 포함한 구강 주위 근육군 간의 불균형, 빨기 습관과 같은 구강 악습관 등이 알려져 있다[5]. 급속 상악 확장은 협착된 상악궁이나 깊은 경구개 그리고 이에 기인한 반대교합이나 총생을 가지는 소아 청소년 환자들에서 흔히 시행되는 임상적인 술식이다[3]. 상악 확장 치료 후에는 주로 정중 구개 봉합에 인접한 비강저에서 비강폭이 증가하게 되고 비강 외벽이 외측으로 이동함에 따라 비강 내부 용량이 증가하게 된다[6,7]. 급속 상악 확장 이후 인두 기도의 변화를 측정한 Buccheri 등(2004) [8]의 연구에서는 상악의 확장 이후 인두 내강 부피의 증가와 함께 비호흡이 개선됨을 함께 확인한 바 있으며 이외의 여러 연구들에서도 상악 확장 이후 비강 폭이 증가함과 함께 비강 기도 저항이 감소하는 결과를 보고한 바 있다[9,10].

전산유체역학은 컴퓨터를 이용하여 Navier-Stokes 방정식과 같은 유체의 운동을 표현하는 방정식을 여러 수치 해석 기법을 이용하여 계산함으로써 유체의 흐름을 수치적으로 표현하는 기술이다[11]. 이 기술은 물리적인 실험을 대체할 수 있는 방법으로써 다양한 공학 분야에서 널리 사용되어 왔고 최근에는 생체 의학 연구 분야에서도 자주 사용되고 있는 분석 방법이다[12]. 전산유체역학은 대상이 되는 유동 모델에 대해 여러 유동 관련 변수들에 대한 예측 및 계산을 가능하게 하며 대표적으로는 유체의 압력이나 유속과 같은 변수들을 측정할 수 있다[13]. 또한 전산유체역학 분석이 완료되면 관련 유동 변수들에 대한 계산 결과를 도표화하여 추출할 수 있으며 또한 모델 내에서 흐름 특성을 애니메이션을 포함한 여러 시각화 도구를 이용하여 표현할 수 있다[12]. 전산유체역학은 이전의 연구들에서 비강을 포함한 상기도에서의 공기 유동 해석을 위해 사용된 바 있다. Suga 등(2021) [14]은 폐쇄성 수면 무호흡 환자에서 하악 전방유도 장치 사용 이후 상기도 내 공기 유동의 개선을 전산유체역학을 이용하여 확인하였으며 Kim 등(2015) [15]은 폐쇄성 수면 무호흡 환자에서 상하악 전진술 후 상기도 내 폐쇄의 개선 여부를 전산유체역학적 방법으로 연구한 바 있다.

상악 확장과 관련된 이전의 여러 연구들에서 급속 상악 확장은 골격성 및 치아치조성 확장 효과에 더해 비강 기도의 저항을 감소시킴으로써 구호흡 습관 및 수면 호흡 장애를 개선시킨다는 결과를 보인 바 있으나 저속 상악 확장의 경우에는 관련된 연구가 거의 시행된 바 없다. 또한 상악 확장과 비호흡 기능간의 관계에 대해 조사한 대부분의 연구들에서는 CBCT를 이용하여 상기도의 폐쇄여부를 확인하거나 비기압계나 음향 비강 통기도 검사기를 이용하여 비저항이나 비강의 부피를 측정하는 데 그쳤다. 전산유체역학을 이용하여 상악 확장 이후의 상기도 내 공기 유동의 변화를 조사한 소수의 연구들은 급속 상악 확장을 시행한 경우만을 대상으로 하였으며 국내에서는 상악 확장을 실시한 소아청소년을 대상으로 전산유체역학 분석을 실시한 연구가 거의 시행된 바 없다. 따라서 본 연구에서는 상악 확장 치료를 받은 소아청소년에서 급속 확장과 저속 확장의 두 확장 유형에 따른 확장 전후의 상기도 내 공기 유동 변화를 전산유체역학을 이용하여 분석하고 그 결과를 비교하고자 한다.

II. 대상 및 방법

1. 연구 대상

전북대학교 소아치과에서 협착된 상악궁에 대해 상악 확장 치료를 받았고 교정 치료 전 호흡 관련 문제를 가지고 있었던 환자들 중 상악 확장의 속도가 다른 환자 2인을 선정하였다. 한명의 환자에서는 급속 상악 확장(Rapid Maxillary Expansion, RME: 2turns/day, 0.5mm/day)이 실시되었고 다른 한명의 환자에서는 저속 상악 확장(Slow Maxillary Expansion, SME: 2 turns/week, 0.5mm)이 실시되었다[5]. 상악궁은 교정 치료 전 평가하는 intermolar width를 이용하여 36mm 보다 작을 경우 협착된 상악으로 평가하였으며 호흡 관련 문제는 구호흡 습관과 같은 호흡과 관련된 환자의 주관적인 증상 여부와 Pediatric Sleep Questionnaire(PSQ) scale 혹은 무호흡-저호흡 지수(Apnea-Hypopnea Index, AHI)와 같은 호흡 문제와 관련된 객관적인 수치를 함께 이용하여 평가하였다[16].

PSQ scale은 Chervin 등(2000) [17]에 개발된 수면 호흡 장애와 관련된 22개의 질문으로 구성된 설문지의 응답 내용을 기반으로 산출되는 지표이다. Cut-off 0.33을 기준으로 이보다 낮을 경우 정상으로, 이와 같거나 높을 경우 수면호흡장애 위험군으로 분류되며 2~18세의 소아청소년에서 수면다원검사가 임상적으로 어려운 경우 이를 대체할 수 있는 수단으로 사용이 가능하다[18].

무호흡-저호흡 지수는 폐쇄성 수면 무호흡의 진단 기준으로 사용되는 지표로써 소아에서는 1이상일 경우 폐쇄성 수면 무호흡에 해당한다[19]. 무호흡-저호흡 지수는 휴대용 간이수면검사 장비(Embletta^® MPR, Natus Medical Inc., California, USA)를 사용하여 측정하였다. 해당 장비는 무호흡-저호흡 지수를 비롯하여 산소 불포화지수(oxygen desaturation index, ODI), 각성 지수(autonomic arousal index), 코골이 시간의 비율, 평균 산소포화도, 최저 산소 포화도 등을 함께 측정할 수 있는 기기로써 교정 치료 시작 전 수면 중 호흡 문제 여부를 평가하기 위해 실시하였다[20]. 본 연구는 전북대학교병원 기관생명윤리위원회로부터의 승인 하에 이루어졌다(IRB File No. CUH 2024-08-055).

2. 연구 방법

상악 확장 치료 전과 치료 후 CBCT를 촬영하였다. 급속 확장의 경우 확장 직후 급격한 골격성 확장이 얻어지지만 치료 이후 약 10주간 골격성 재발, 치성적 보상이 발생하며 저속 확장의 경우에는 골격적, 치성적 변화가 유사한 비율로 함께 발생하여 약 10주 이후에는 비슷한 정도의 골격성, 치성적 변화를 보이게 된다[21]. 확장 속도 차이에 따른 치료 전후 촬영 간의 기간 차이로 인한 오류를 최소화하기 위해, 치료 후 발생하는 골격적 및 치성적 변화가 충분히 일어나고, 급속 확장과 저속 확장의 골격적 및 치성적 효과가 비슷해지는 시기인 10주를 넘을 수 있도록 약 3개월 이상의 유지 기간을 거친 후 CBCT를 촬영하였다.

이후 Mimics(Materialize NV, Leuven, Belgium) 소프트웨어를 이용하여 연구 대상으로 선정된 환자의 치료 전후의 CBCT 데이터를 이용하여 비강 기도의 3D model을 형성하였다. 비강 기도의 범위는 이전의 통상적인 연구들에 의거하여 외비공에서부터 후두개 최상방의 수평면을 기준으로 인두기도까지 포함되도록 하였으며 측방으로는 비강을 넘어가지 않도록 추출하였다[22]. 전산유체역학의 특성상 3D model의 geometry 상의 차이는 계산 결과에 보다 더 큰 차이를 유발할 수 있기 때문에 대부분의 비중격 표면 부위 및 치료 전후 CBCT 데이터 상에서 공통으로 나타나는 구조들만을 포함하여 치료 전후의 geometry에 큰 차이가 없도록 segmentation 하였다. Inlet으로 사용될 외비공은 치료 전후 geometry의 형태를 고려하여 수직 혹은 수평의 단일 평면으로 설정하였다. 추출한 Geometry는 동일 소프트웨어를 사용하여 1차적으로 smoothing 및 wrapping의 표면 처리를 실시하여 최종적인 3D model을 형성하였다(Fig. 1,2).

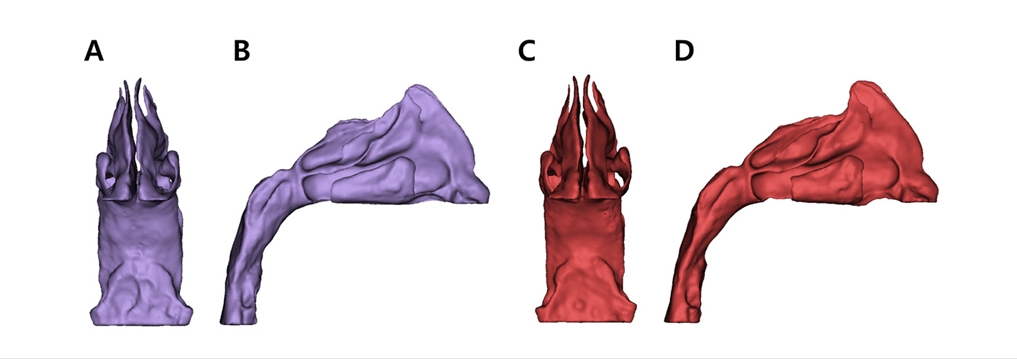
Figure 1.

3D reconstruction models used for CFD analysis of patient who underwent RME; Anterior (A) and Right (B) view of Pre-expansion model and Anterior (C) and Right (D) view of Post-expansion model.

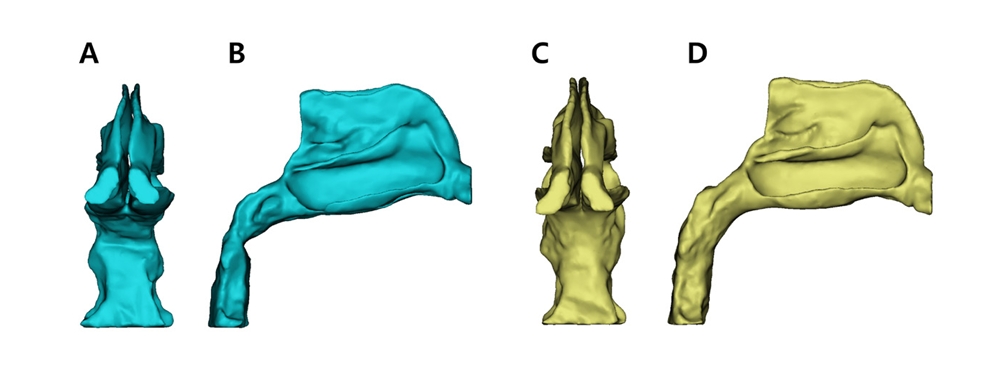
Figure 2.

3D reconstruction models used for CFD analysis of patient who underwent SME; Anterior (A) and Right (B) view of Pre-expansion model and Anterior (C) and Right (D) view of Post-expansion model.

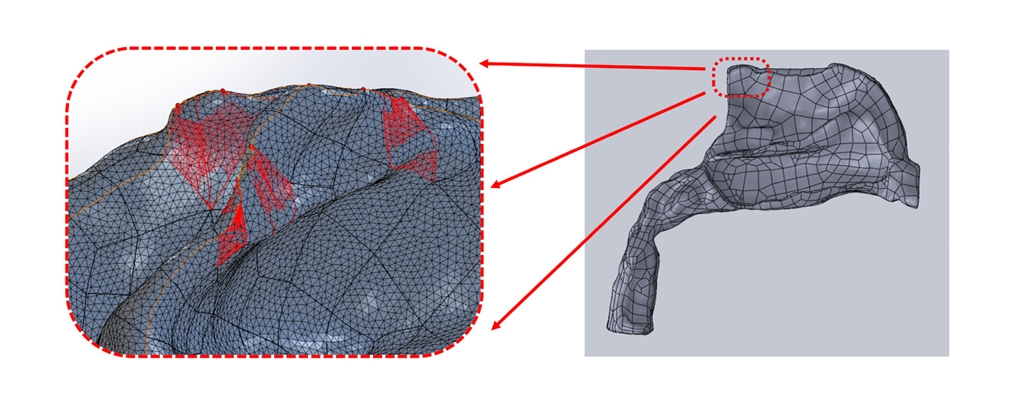
형성한 3D model은 Meshmixer(Autodesk Inc., San Rafael, Calif, USA) 소프트웨어를 이용하여 smoothing 과정을 다시 거친 후 mesh로 분할하였다. Meshmixer 소프트웨어를 이용하여 1차적으로 분할된 mesh는 비강 기도의 복잡한 구조로 인해 표면에서의 mesh 경계상에 많은 오류들이 존재하며 이러한 오류들은 mesh 간의 계산값들을 유기적으로 이용하는 전산유체역학 해석을 방해하는 요소가 된다(Fig. 3). 이에 따라 SolidWorks(Dassault Systems, Vélizy-Villacoublay, France) 소프트웨어를 사용하여 mesh간의 경계를 수정하는 방식으로 분할된 mesh를 안정화시켰다(Fig. 4). 이후 형성된 mesh model을 기반으로 COMSOL multiphysics(COMSOL Inc., Burlington, MA, USA) 소프트웨어를 이용하여 전산유체역학을 실시하였다.

Figure 3.

Surface mesh boundary errors detected in mesh-divided 3D reconstruction model.

Figure 4.

Process of error revision using SolidWorks(Dassault Systems, Vélizy-Villacoublay, France).

유체의 조건은 비압축성의 뉴턴 유체의 특성을 가지는 gas로 설정하였으며 inlet은 외비공으로 설정하고 normal inflow velocity 조건을 부여하였고 outlet인 후두개 직상방 plane에서는 pressure의 조건을 설정하여 해석을 진행하였다. 유량은 10LPM으로 설정하였고 시간을 t, 특정 시간에의 유속을 V_(t), 최대 유속을 V_max, 단위 시간당 호흡 주기의 빈도를 f로 정의하였을 때 이전의 연구를 근거로 다음 수식과 같이 제작된 velocity profile 중 가장 높은 값, 즉 최대 흡기 시의 조건에 대해 해석을 진행하였다[23,24].

V_(t)=V_max sin(2πft)

벽면의 조건은 non-slippery하고 rigid한 조건으로 설정하고 유동 모델은 이전의 연구들을 바탕으로 안정 시 호흡에서 보이는 층류 유동 모델을 사용하였다. 전산유체역학 해석이 완료되고 나면 압력(pressure), 유속(velocity), 벽면 전단응력(wall shear stress, WSS) 등의 유동 관련 변수에 대한 분석을 실시하였다.

III. 결과

1. 연구 대상

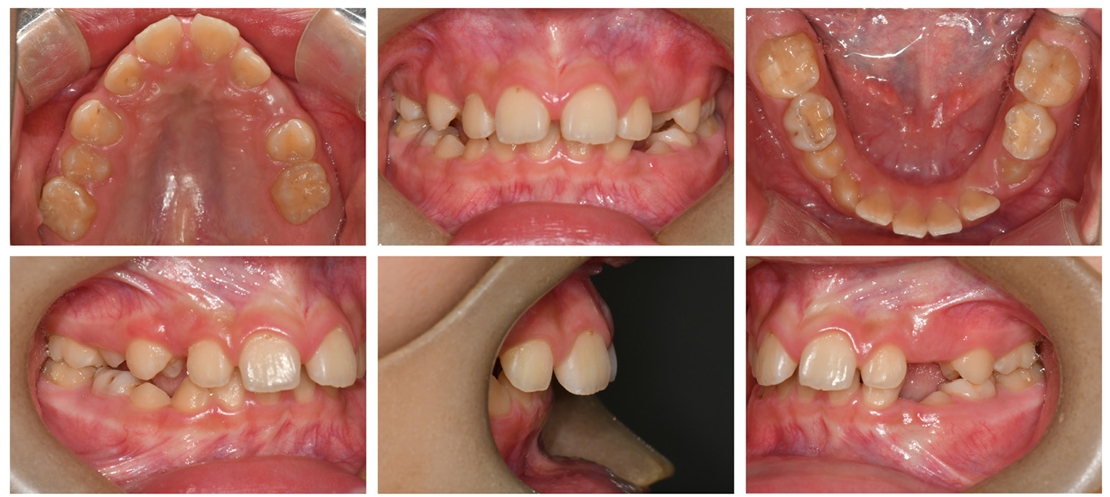
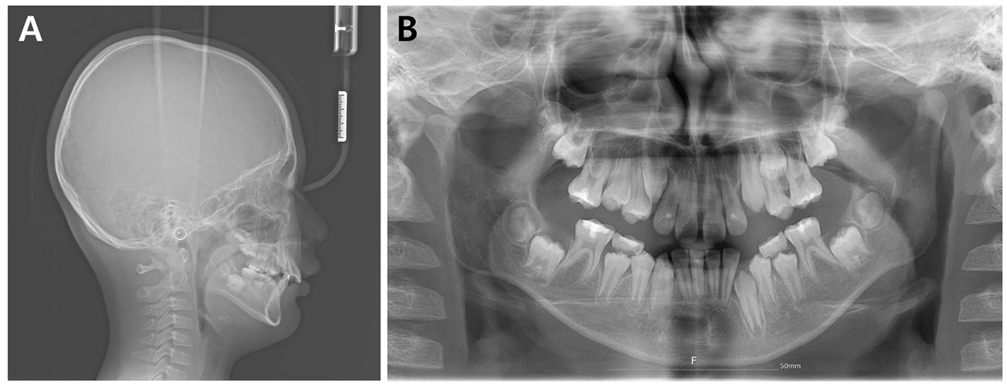
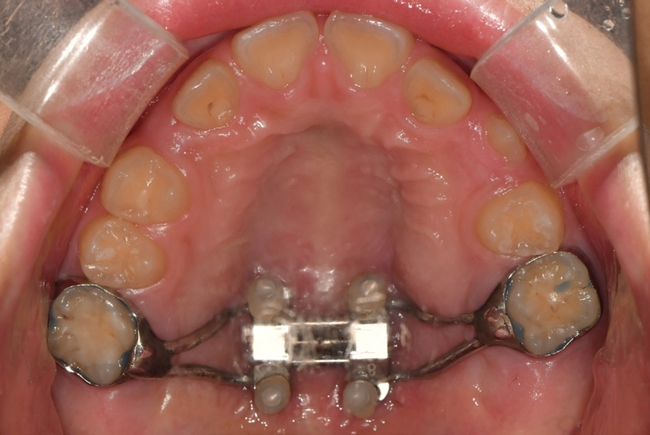
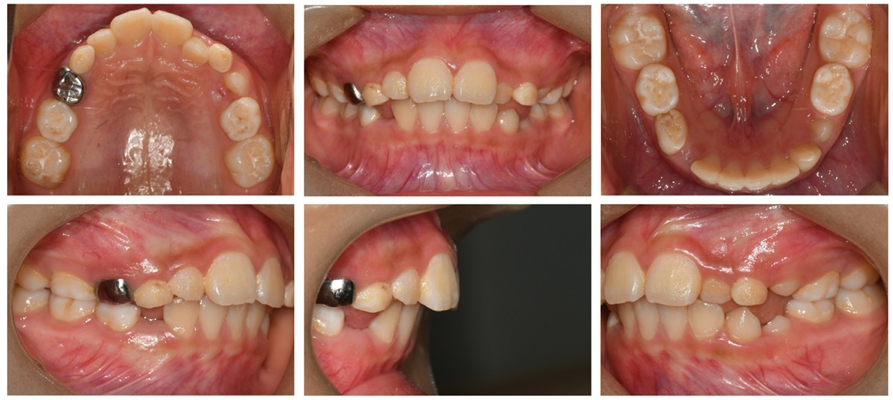
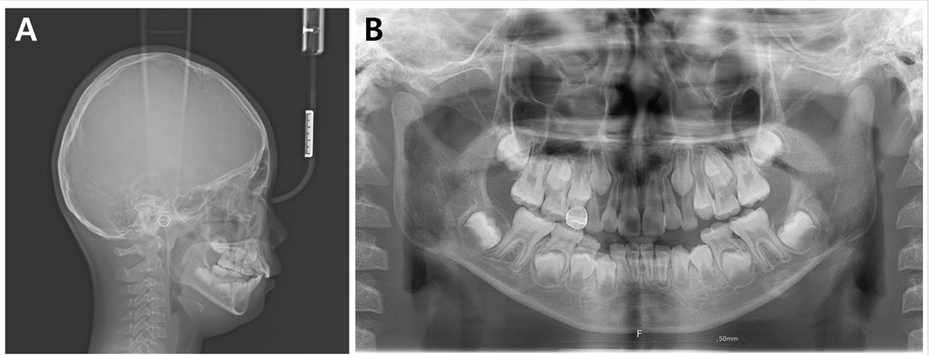
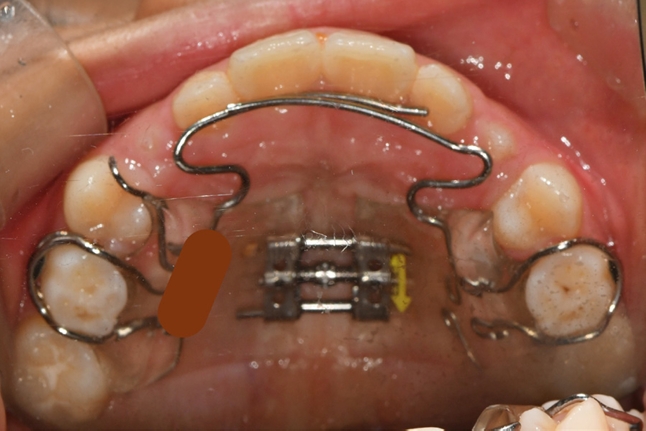
급속 상악 확장 치료를 받은 환자는 10세 남아로 32.1 mm의 intermolar width, 2.1의 무호흡-저호흡 지수, 그리고 구호흡 습관을 가지고 있었다(Fig. 5). 상대적인 하악의 저성장 양상을 동반한 2급의 골격 관계를 보였으며 협착된 상악궁의 개선을 위해 MARPE를 이용하여 급속 확장의 속도로 7mm의 상악 확장을 실시하였다(Fig. 6,7,8).

Figure 5.

Pre-treatment intra-oral photographs of patient who underwent RME.

Figure 6.

Pre-treatment lateral cephalogram (A) and panoramic radiograph (B) of patient who underwent RME.

Figure 7.

Expansion appliance placed in upper dental arch of patient who underwent RME.

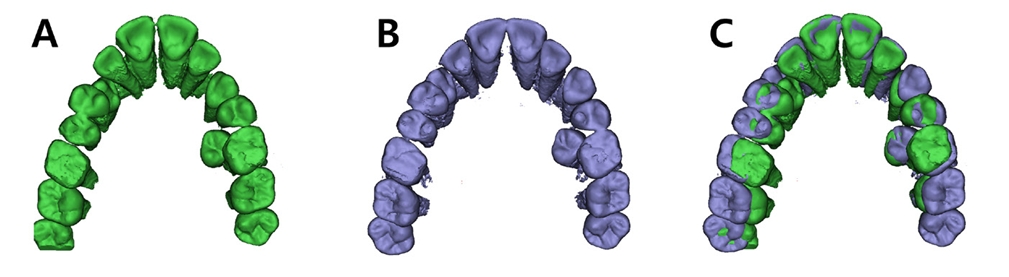
Figure 8.

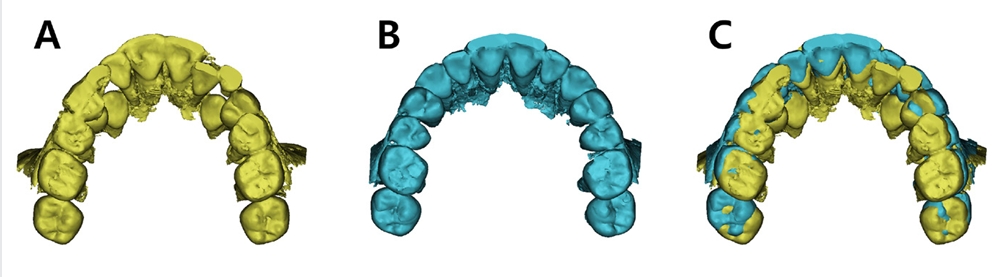
3D reconstruction models of upper dental arches of patient who underwent RME. (A) Pre-expansion. (B) Post-expansion. (C) Superposition of Pre- and Post-expansion.

저속 상악 확장 치료를 받은 환자는 8세 남아로 35.7 mm의 intermolar width, 1.5의 무호흡-저호흡 지수와 함께 구호흡 습관을 가지고 있었다(Fig. 9). 상악에 비해 상대적으로 하악이 후방에 위치한 2급의 골격 관계를 보였으며 협착된 상악궁의 개선을 위해 가철식 장치를 이용하여 저속 확장의 속도로 7mm의 상악 확장을 실시하였다(Fig. 10,11,12).

Figure 9.

Pre-treatment intra-oral photographs of patient who underwent SME.

Figure 10.

Pre-treatment lateral cephalogram (A) and panoramic radiograph (B) of patient who underwent SME.

Figure 11.

Expansion appliance placed in upper dental arch of patient who underwent SME.

Figure 12.

3D reconstruction models of upper dental arches of patient who underwent SME. (A) Pre-expansion. (B) Post-expansion. (C) Superposition of Pre- and Post-expansion.

2. 급속 상악 확대 전후의 상기도에 대한 전산유체역학 해석

상기도 내 공기의 압력 분포에 대해 확장 전 모델에서는 비강의 전방부에서 높은 압력 분포가 관찰되었으며 비강의 후방부에서 급격한 압력의 감소가 관찰된다(Fig. 13A). 이에 반해 확장 후 모델에서는 비강의 전방부에서 상대적으로 낮은 정도의 압력이 분포하고 있으며 압력의 강하는 비강을 따라 상대적으로 완만하게 이루어진다(Fig. 13B). 상기도 내에서 관찰되는 최대 압력 값은 확장 전에는 15.41Pa을 보였으나 확장 후에는 11.45Pa로 감소하였다.

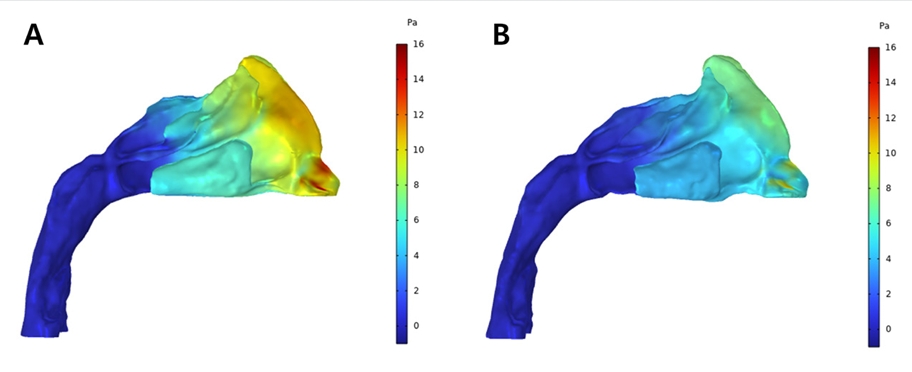
Figure 13.

Pressure profile from CFD analysis of patient who underwent RME; Pre-expansion (A) and Postexpansion (B).

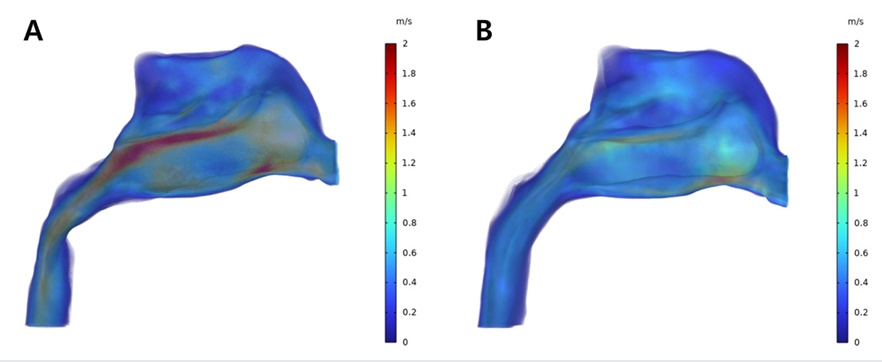
상기도 내에서 흐르는 공기의 유속은 확장 전 모델에서는 비강의 전방부와 비강과 인두기도의 경계부위, 즉 후비공 인근의 영역에서 높은 수치가 관찰되었다(Fig. 14A). 확장 후 모델에서는 전반적으로 유속의 수준이 감소하였고 특히 후비공 인근의 영역에서 관찰되는 높은 유속 분포가 많이 감소하였음을 볼 수 있다(Fig. 14B). 최대 유속값은 확장 전 모델에서는 3.80m/s이였으며 확장 후 모델에서는 3.53m/s로 감소하였다.

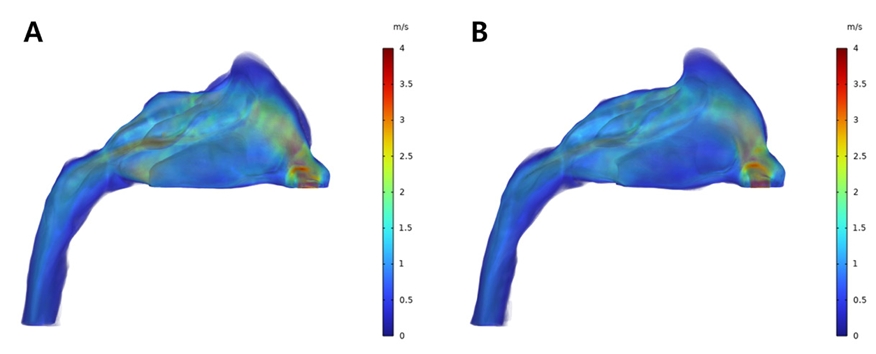
Figure 14.

Velocity profile from CFD analysis of patient who underwent RME; Pre-expansion (A) and Post-expansion (B).

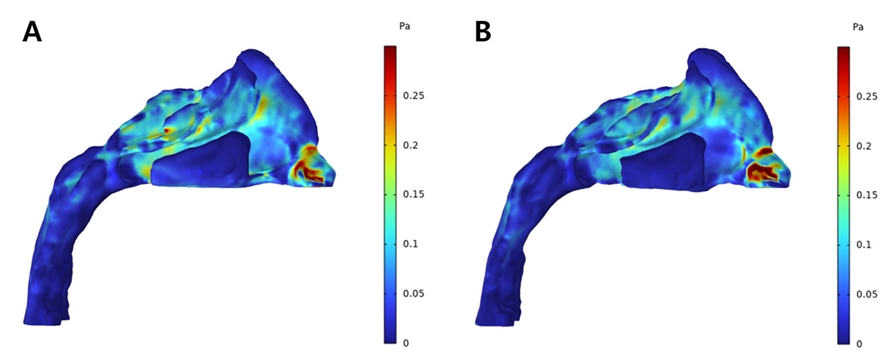
확장 전 모델에서 상기도 내부의 벽면 전단응력 수치는 이전의 압력, 유속의 결과와 유사하게 비강의 전방부에서 높은 정도의 수치를 보였고 비강의 중앙부위에서 후비공에 이르는 영역까지 상대적으로 높은 전단응력 분포가 관찰되었다(Fig. 15A). 확장 후 모델에서는 비강 전반적으로 확장 전에 비해 낮은 정도의 전단응력 분포를 보이고 있으며 최대 전단응력 수치 역시 확장 전 0.56Pa에 비해 0.47Pa로 감소된 결과를 보였다(Fig. 15B).

Figure 15.

Wall shear stress profile from CFD analysis of patient who underwent RME; Pre-expansion (A) and Post-expansion (B).

3. 저속 상악 확대 전후의 상기도에 대한 전산유체역학 해석

저속 상악 확장을 실시한 환자의 확장 전 모델에서는 비강의 전방부에서 높은 압력이 분포하고 있고 외비공에서 후비공에 이르기까지 상대적으로 가파른 정도의 압력 감소를 보였다(Fig. 16A). 확장 후 모델에서도 가장 높은 압력은 외비공 인근의 영역에 분포하고 있었으나 그 정도가 확장 전에 비해 낮은 수준이였으며 공기의 흐름에 따른 압력의 변화 역시 완만한 감소 양상을 보이고 있다(Fig. 16B). 최대 압력값은 확장 전에는 8.12Pa을 보였으며 확장 후에는 3.44Pa의 수치를 보였다.

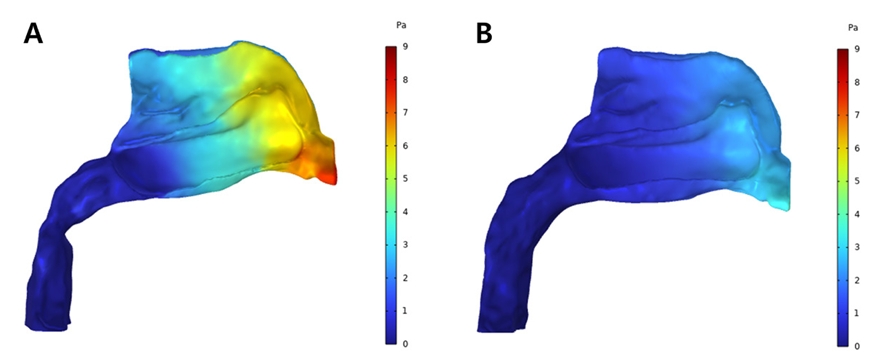
Figure 16.

Pressure profile from CFD analysis of patient who underwent SME; Pre-expansion (A) and Post-expansion (B).

저속 확장 전 모델에서 유속은 전후방적으로는 비강의 중앙부위에서 후비공에 이르는 영역까지 분포하고 있으며 수직적으로는 비강의 중하방 부위에서 높은 수치를 보이고 있다(Fig. 17A). 이러한 높은 유속 분포 부위에 대해 확장 후 모델에서는 전체적인 유속의 감소 양상이 관찰되었으며 확장 전 상기도에서 관찰된 1.99m/s의 최대 유속값은 확장 후 1.55m/s로 감소하였다(Fig. 17B).

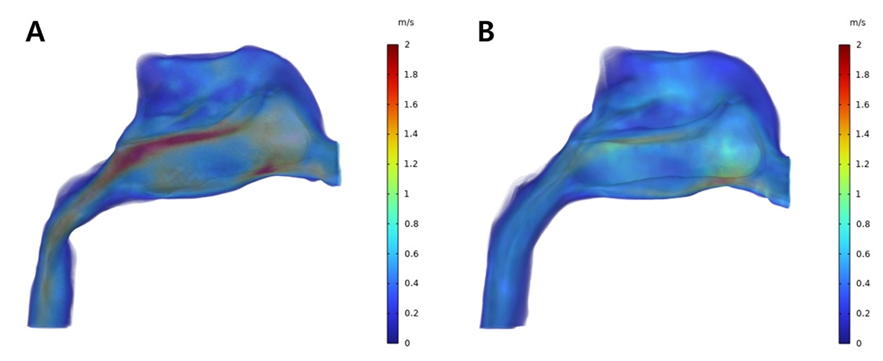
Figure 17.

Velocity profile from CFD analysis of patient who underwent SME; Pre-expansion (A) and Post-expansion (B).

벽면 전단응력은 저속 확장 전 모델에서는 상기도 중비강의 전반적인 영역에서 높은 수치를 보였고 특히 비강의 중하방 부위에서 높은 응력 분포 결과를 보였다(Fig. 18A). 이러한 결과에 대해 확장 후 모델에서는 이전의 결과들과 마찬가지로 전체적인 영역에서 감소된 응력 분포를 보였고 최대 전단응력 수치 역시 확장 전 0.27Pa에서 확장 후 0.13Pa로 감소한 결과를 보였다(Fig. 18B).

Figure 18.

Wall shear stress profile from CFD analysis of patient who underwent SME; Pre-expansion (A) and Post-expansion (B).

IV. 고찰

본 연구에서는 서로 다른 유형의 상악 확장을 시행 받은 두 환자를 대상으로 확장 전후에 대한 전산유체역학적 분석을 실시함으로써 상기도 내 압력, 유속, 벽면 전단응력 분포 결과를 수치화 및 시각화하여 도출하였다.

비강 환기 상태의 객관적 평가를 위해 이전부터 사용되어왔던 전방 비강 통기도 검사는 외비공과 후비공 사이의 압력차이를 이용하는 검사 방법이며 Mo 등(2010) [25]의 연구에서는 상기도 내 공기 유동에서 관찰되는 최고 압력과 최저압력의 차이 즉 압력 강하 정도는 호흡 시에 발생되는 일종의 기도 저항이며 기도의 형태적 특성에 기인할 수 있는 모든 요소를 종합적으로 반영하는 지표로 이용될 수 있을 것이라고 하였다[26]. 종합적으로 상기도 내부의 공기 흐름에 대한 전산유체역학적 평가에서 압력은 환기 상태 평가에 있어 매우 중요한 지표임을 알 수 있다. 본 연구에서는 inlet을 외비공으로 설정하고 outlet을 후두개 직상방의 평면으로 설정하였으며 공기 유동을 외비공으로부터 끌어오는 과정, 즉 흡기 과정 중 최대 흡기 시를 대상으로 분석을 진행하였다. 이에 따라 비강 내부의 공기압은 유동 과정동안 다양한 변화양상을 보일 수 있으나 결과적으로는 감소하게 된다. 이 때 감소의 정도는 비강 내부의 형태적 구조에 따라 결정되며 비강이 좁아지는 위치에서 압력은 급격하게 감소한다[27]. 급속 상악 확장을 시행한 환자의 확장 전 모델에 대한 전산유체역학 분석 결과 비강의 전방부에서 높은 압력 분포를 보였고 비강의 전방부와 후비공 직전의 영역에서 급격한 압력의 변화양상을 보였다. 저속 상악 확장을 시행한 환자의 확장 전 모델에서는 비강의 전방부에서 상대적으로 높은 압력 분포와 함께 급격한 압력의 변화를 보였다. 즉, 압력에 대한 전산유체역학 분석 결과를 통해 급속 상악 확장을 시행한 환자에서는 비강의 전방부와 후비공 영역, 저속 상악 확장을 시행한 환자에서는 비강의 전방부에서 협착부위가 존재함을 알 수 있다. 또한 두 환자 모두에서 확장 후 모델에서는 점진적인 압력의 감소 양상을 보였기에 이를 통해 확장의 유형에 관계없이 상악 확장 이후 상기도상의 협착이 개선되었음을 알 수 있다.

유속에 대한 본 연구 결과, 급속 상악 확장을 시행한 환자에서는 확장 전 압력 분포와 유사한 위치인 비강의 전방부와 후비공 인근의 영역에서 상대적으로 높은 유속 분포를 보였지만 저속 상악 확장을 시행한 환자에서는 수직적으로 비강의 중하방 영역에서 높은 유속 분포를 보였다. 비강 내에서 유속은 유로의 단면적에 따라 변화하게 되며 이전의 연구에서 Downing 과 Ku(1997) [28]는 전산유체역학 모델에서 유체는 좁아진 유로를 지날 때 유속이 증가한다고 하였다[26]. 유속의 분포를 시각화할 수 있는 전산유체역학을 사용함으로써 저속 확장을 시행 받은 환자에서 확장 전 압력 분포 결과에서 확인된 비강의 전방부 이외에 수직적으로 비강의 중하방 부위에서도 협착부위가 존재함을 확인할 수 있었다. Minami 등(2020) [29]의 연구에서는 기도 내부의 단면적과 유속 사이의 음의 상관관계를 확인하였고 또한 기도 내 최대 유속과 AHI 간의 상관관계를 확인하여 전산유체역학을 통해 평가된 유속이 상기도 전체를 평가하는데 사용될 수 있음을 보여주었다.

전산유체역학은 상기도를 평가하는 다른 도구들과는 달리 기도 내 공기 흐름에 의해 기도 내벽에서 발생하는 벽면 전단응력을 평가할 수 있다. 벽면 전단응력은 비강내 점막의 기계적 수용체의 활성과 비례하며 이를 통해 환자에 의해 주관적으로 평가되는 비호흡의 증상과 상관관계를 가지게 된다[26]. 벽면 전단응력은 주로 유로의 내벽과 공기 유동의 상호작용이 큰 곳이나 유동의 방향이 급격하게 변화하는 곳에서 증가하게 된다[30]. 벽면 전단응력은 또한 상기도의 면역 체계에 있어 매우 중요한 요소이다. 과도한 벽면 전단응력은 비강 내부에서 큰 유속을 유발하게 되고 이는 비강 점막의 미세혈관 손상의 원인이 될 수 있으며 상피세포층의 기능에도 부정적으로 영향을 미칠 수 있다[31]. 본 연구 결과 급속 상악 확장을 시행한 환자의 확장 전 모델에서는 비강의 전방부와 후비공 인근의 영역에서 높은 정도의 벽면 전단응력이 분포하였으나 확장 후 후비공 영역의 높은 전단응력 분포는 감소하였다. 저속 확장을 시행한 환자에서는 확장 전 유속 분포와 유사한 위치에서 높은 전단응력 분포를 보였으나 확장 후 개선된 결과를 보였다. 확장 유형과 관계없이 두 환자 모두에서 확장 이후 비강 내 벽면 전단응력 수준은 감소하였으며 이는 상악 확장이 협착부위의 개선에 더해 비강 점막의 보호 기능을 증진시키는데 도움이 될 수 있음을 시사한다.

급속 상악 확장은 큰 힘이 직접적으로 봉합부에 전달되고 이에 따라 확장 초기에는 봉합부가 우선적으로 개방되어 골격성 확장이 주로 발생하게 된다. 이 후 유지기간동안 지속적으로 구개 하방부에서는 골격성 재발이 발생하게 되어 결과적으로는 골격성 확장과 치아치조성 확장이 비슷한 비율을 가지게 된다. 이에 반해 저속 상악 확장에서는 생리적인 속도로 상대적으로 천천히 확장을 시행하게 됨으로써 확장 초기부터 골격성 확장과 치아치조성 확장이 비슷한 비율로 발생하게 되며 이는 확장이 완료될 때까지 유지되게 된다[21]. Greenbaum 과 Zachrisson(1982) [32]은 급속 상악 확장과 저속 상악 확장이 치주 조직에 미치는 영향에는 유의한 차이가 없다는 결과를 보였으며 상악 제1대구치에서 부착상실이 발생한 대부분의 경우에서 급속 상악 확장이 시행되었음을 보고한 바 있다. 상악 확장 속도에 따른 치아치조성, 골격성 효과 및 상기도에 대한 영향을 분석한 Kim 등(2023) [5]의 연구에 의하면 저속 상악 확장은 유의미한 치아 치조성 맟 골격성 확장 효과에 더해 상기도 및 상악동의 부피 변화에 대해서도 유의미한 효과를 보인다고 하였다. 또한 급속 상악 확장과 그 효과를 비교해 보았을 때 통계적으로 유의한 차이를 보이지 않았다는 결과를 보고하였다. 두 확장 유형이 상기도의 부피와 같은 물리적 특성에 미친 영향을 평가하였던 이전의 연구 결과에 더해 본 연구에서는 전산유체역학을 이용하여 공기의 유동을 분석함으로써 두 확장 유형이 상기도 내 공기의 흐름, 즉 상기도의 기능적인 측면에 대한 개선 여부를 분석하고자 하였으며 서로 다른 유형의 상악 확장을 시행한 두 환자 모두에서 공기 유동이 개선된 결과를 보였다.

전산유체역학은 눈에 보이지 않는 유체 유동의 특성을 시각화할 수 있다는 점에서 다른 평가방법에 비해 큰 장점을 가진다[12]. 전산유체역학을 적용하면 유동 관련 변수들의 모델 내 분포에 대한 시각화 영상을 얻을 수 있으며 이를 통해 상기도의 평가를 위해 기존에 사용되었던 CBCT를 이용한 상기도의 형태적인 평가에서는 발견할 수 없었던 비강내 폐쇄부위를 추가로 발견할 수 있게 되었다[33]. 환자 개개인의 상기도 3D 모델을 기반으로 전산유체역학 분석을 시행한다면 환자에 따른 상기도 내 폐쇄부위의 확인이 가능하고 이를 통해 원인 부위에 적합한 치료 방법을 선택함으로써 환자 맞춤형 치료 전략 수립에 도움이 될 것으로 생각된다.

본 연구는 확장 유형당 한명의 환자를 대상으로 하였다는 점에서 충분한 표본 수의 부족이라는 한계점이 있으며 이에 따라 본 연구결과를 일반화하기는 어렵다. 그럼에도 본 연구는 국내에서 거의 시행되지 않았던 소아청소년에서의 상악 확장에 따른 상기도 내 공기 유동 분석을 전산유체역학을 이용하여 실시함으로써 향후 국내에서 진행될 수 있는 후속 연구들에 대한 기반 자료를 제공하였으며 또한 서로 다른 확장 유형을 사용한 환자 모두에서 상기도 내 공기 유동이 확장 이후 개선되었다는 결과를 확인하였다는 점에서 그 의의가 있다. 본 연구에서 수립된 상기도에 대한 전산유체역학 적용 과정을 기반으로 추후 진행될 연구에서는 충분한 표본 수의 확보를 통해 두 확장 유형이 압력, 유속, 벽면 전단응력과 같은 유동 관련 변수들에 대해 어느 정도의 영향을 미치는지에 대한 통계적인 비교 분석이 시행되어야 할 것이다. 이에 더해 전산유체역학의 시각화의 장점을 활용하여 두 확장 유형이 각각 상기도 내의 어느 위치에서 주된 공기 유동의 개선 효과를 보였는지에 대한 비교 분석 역시 추후에 시행될 수 있을 것으로 생각된다.

Notes

이해상충(Conflicts of Interest)의 유무

The authors have no potential conflicts of interest to disclose.

FUNDING

This paper was supported by Fund of Biomedical Research Institute, Jeonbuk National University Hospital.

Acknowledgements

Tae-Hyun Kim and Kyung-Ho Lee equally contributed as first authors to this work.

References

1. McNamara JA. Influence of respiratory pattern on craniofacial growth. Angle Orthod 1981;51:269–300. https://doi.org/10.1043/0003-3219(1981)051%3C0269:IORPOC%3E2.0.CO;2.

2. Moss-Salentijn L, Melvin L. Moss and the functional matrix. J Dent Res 1997;76:1814–1817. https://doi.org/10.1177/00220345970760120201.

3. Kiliç N, Oktay H. Effects of rapid maxillary expansion on nasal breathing and some naso-respiratory and breathing problems in growing children: a literature review. Int J Pediatr Otorhinolaryngol 2008;72:1595–1601. https://doi.org/10.1016/j.ijporl.2008.07.014.

4. Lee MJ, Kim JG, Yang YM, Baik BJ. Effects of mouth breathing on facial skeletal morphology. J Korean Acad Pediatr Dent 2012;39:339–347.

5. Kim NW, Lee DW, Kim JG, Yang YM. Three Dimensional Skeletal, Dentoalveolar and Airway Space Changes after Slow Maxillary Expansion in Children. J Korean Acad Pediatr Dent 2023;50:155–167. https://doi.org/10.5933/JKAPD.2023.50.2.155.

6. Wertz RA. Skeletal and dental changes accompanying rapid midpalatal suture opening. Am J Orthod 1970;58:41–66. https://doi.org/10.1016/0002-9416(70)90127-2.

7. Haas AJ. Rapid expansion of the maxillary dental arch and nasal cavity by opening the midpalatal suture. Angle Orthod 1976;31:73–90. https://doi.org/10.1043/0003-3219(1961)031%3C0073:REOTMD%3E2.0.CO;2.,.

8. Buccheri A, Dilella G, Stella R. Rapid palatal expansion and pharyngeal space. Cephalometric evaluation. Prog Orthod 2004;5:160–171.

9. Hershey HG, Stewart BL, Warren DW. Changes in nasal airway resistance associated with rapid maxillary expansion. Am J Orthod 1976;69:274–284. https://doi.org/10.1016/0002-9416(76)90076-2.

10. Wertz RA. Changes in nasal airflow incident to rapid maxillary expansion. Angle Orthod 1968;38:1–11. https://doi.org/10.1043/0003-3219(1968)038%3C0001:CINAIT%3E2.0.CO;2.

11. Kundu PK, Cohen IM, Dowling DR. Fluid mechanics. In : Hu HH, ed. Computational fluid dynamics 5th edth ed. Elsevier; 2012. p. 421–472.

12. Faizal W, Ghazali NN, Khor C, Badruddin IA, Zainon MZ, Yazid AA, et al. Computational fluid dynamics modelling of human upper airway: A review. Comput Methods Programs Biomed 2020;196:105627. https://doi.org/10.1016/j.cmpb.2020.105627.

13. Bailie N, Hanna B, Watterson J, Gallagher G. An overview of numerical modelling of nasal airflow. Rhinology 2006;44:53–57.

14. Suga H, Iwasaki T, Mishima K, Nakano H, Ueyama Y, Yamasaki Y. Evaluation of the effect of oral appliance treatment on upper-airway ventilation conditions in obstructive sleep apnea using computational fluid dynamics. CRANIO^® 2021;39(3):209–217. https://doi.org/10.1080/08869634.2019.1596554.

15. Kim HH, Suh SH, Choi JY, Kim TY. Flow analyses of upper airway before and after maxillomandibular advancement surgery for obstructive sleep apnea patient. Transactions of the KSME B 2015;39:443–448. https://doi.org/10.3795/KSME-B.2015.39.5.443.

16. McNamara JA, Brudon WL. Orthodontic and orthopedic treatment in the mixed dentition 1st edth ed. Needham Pr; 1993.

17. Chervin RD, Hedger K, Dillon JE, Pituch KJ. Pediatric sleep questionnaire (PSQ): validity and reliability of scales for sleep-disordered breathing, snoring, sleepiness, and behavioral problems. Sleep Med 2000;1:21–32. https://doi.org/10.1016/S1389-9457(99)00009-X.

18. Yang YM. Sleep Disordered Breathing in Children. J Korean Acad Pediatr Dent 2022;49:357–367. https://doi.org/10.5933/JKAPD.2022.49.4.357.

19. Savini S, Ciorba A, Bianchini C, Stomeo F, Corazzi V, Vicini C, et al. Assessment of obstructive sleep apnoea (OSA) in children: an update. Acta Otorhinolaryngol Ital 2019;39:289–297. https://doi.org/10.14639/0392-100x-n0262.

20. Moon SY, Lee DW, Kim JG, Yang YM. Assessment of Predicting Factors for Pediatric Sleep Disordered Breathing. J Korean Acad Pediatr Dent 2020;47:377–388. https://doi.org/10.5933/JKAPD.2020.47.4.377.

21. Proffit WR, Fields H, Larson B, Sarver DM. Contemporary orthodontics 6th edth ed. Amsterdam: Elsevier; 2021.

22. Chang KK, Kim KB, McQuilling MW, Movahed R. Fluid structure interaction simulations of the upper airway in obstructive sleep apnea patients before and after maxillomandibular advancement surgery. Am J Orthod Dentofacial Orthop 2018;153:895–904. https://doi.org/10.1016/j.ajodo.2017.08.027.

23. Ormiskangas J, Valtonen O, Kivekäs I, Dean M, Poe D, Järnstedt J, et al. Assessment of PIV performance in validating CFD models from nasal cavity CBCT scans. Respir Physiol Neurobiol 2020;282:103508. https://doi.org/10.1016/j.resp.2020.103508.

24. Soni B, Aliabadi S. Large-scale CFD simulations of airflow and particle deposition in lung airway. Comput Fluids 2013;88:804–812. https://doi.org/10.1016/j.compfluid.2013.06.015.

25. Mo SS, Ahn HT, Lee JS, Chung YS, Moon YS, Pae EK, et al. Morphological characteristics of the upper airway and pressure drop analysis using 3D CFD in OSA patients. Korean J Orthod 2010;40:66–76. https://doi.org/10.4041/kjod.2010.40.2.66.

26. Moreddu E, Meister L, Philip-Alliez C, Triglia JM, Medale M, Nicollas R. Computational fluid dynamics in the assessment of nasal obstruction in children. Eur Ann Otorhinolaryngol Head Neck Dis 2019;136:87–92. https://doi.org/10.1016/j.anorl.2018.11.008.

27. Xavier R, Menger DJ, de Carvalho HC, Spratley J. An overview of computational fluid dynamics preoperative analysis of the nasal airway. Facial Plast Surg 2021;37:306–316. https://doi.org/10.1055/s-0041-1722956.

28. Downing J, Ku D. Effects of frictional losses and pulsatile flow on the collapse of stenotic arteries. J Biomech Eng 1997;119:317–324. https://doi.org/10.1115/1.2796096.

29. Minami AY, Sugiyama T, Iwasaki T, Yamasaki Y. Primary site identification in children with obstructive sleep apnea by computational fluid dynamics analysis of the upper airway. J Clin Sleep Med 2020;16:431–439. https://doi.org/10.5664/jcsm.8224.

30. Tan J, Han D, Wang J, Liu T, Wang T, Zang H, et al. Numerical simulation of normal nasal cavity airflow in Chinese adult: a computational flow dynamics model. Eur Arch Otorhinolaryngol 2012;269:881–889. https://doi.org/10.1007/s00405-011-1771-z.

31. Chen S, Wang J, Xi X, Zhao Y, Liu H, Liu D. Rapid maxillary expansion has a beneficial effect on the ventilation in children with nasal septal deviation: A computational fluid dynamics study. Front Pediatr 2022;9:718735. https://doi.org/10.3389/fped.2021.718735.

32. Greenbaum KR, Zachrisson BU. The effect of palatal expansion therapy on the periodontal supporting tissues. Am J Orthod 1982;81:12–21. https://doi.org/10.1016/0002-9416(82)90283-4.

33. Iwasaki T, Saitoh I, Takemoto Y, Inada E, Kanomi R, Hayasaki H, et al. Improvement of nasal airway ventilation after rapid maxillary expansion evaluated with computational fluid dynamics. Am J Orthod Dentofacial Orthop 2012;141:269–278. https://doi.org/10.1016/j.ajodo.2011.08.025.

Article information Continued

Articles published in the JKDA are open-access, distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by-nc/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.